2.5 Establishment of Pressure Drop Model

At present, the most commonly used formulas for calculating pressure drop in oil and gas mixed transportation are the Dukler I method, Dukler II method, and Beggs Brill method. These three models are established based on the assumptions of homogeneous flow, phase separated flow, and flow pattern, respectively.This article compares the Dukler I method and the Dukler II method to explore a suitable pressure drop prediction model for heavy oil mixed with gas flow.

(1) Dukler I and Dukler II Methods

The Dukler I method assumes that the gas and liquid phases are uniformly mixed in the pipeline, and hydraulic calculations are performed using the method of single-phase pipe flow. The parameters related to single-phase fluid in the formula are replaced with the average parameters of gas-liquid mixed flow. The pressure drop in the pipeline is calculated using Darcy's formula.

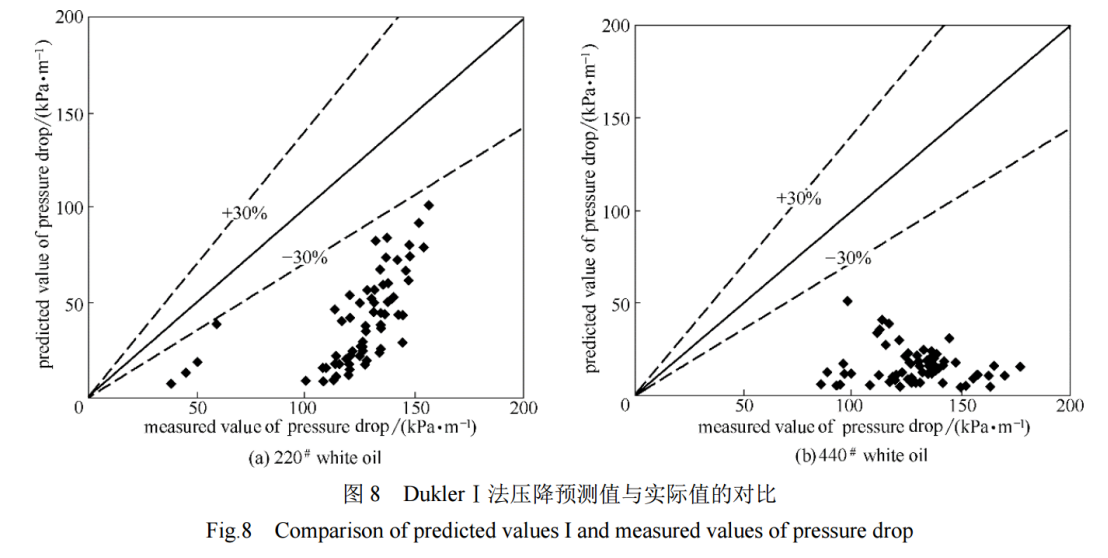
The Dukler I method (predicted value I) was used to calculate the pressure drop of two types of white oil. The comparison between the predicted and measured values is shown in Figure 8.

The Dukler II method believes that gas-liquid two-phase flow can only be approximated as phase slip free when the flow velocity is very high, while in actual pipelines, the flow velocity of gas-liquid two-phase flow is generally different, and there is phase slip between the two phases.Using the similarity theory, assuming that the sliding ratio between the gas-liquid phases does not change along the length of the tube, a pressure drop calculation method is proposed when there is slippage between phases.The pressure drop is also calculated using Darcy's formula. The density of gas-liquid mixture is calculated as follows.

At this point, the hydraulic friction coefficient of gas-liquid horizontal mixed transportation is calculated as follows：

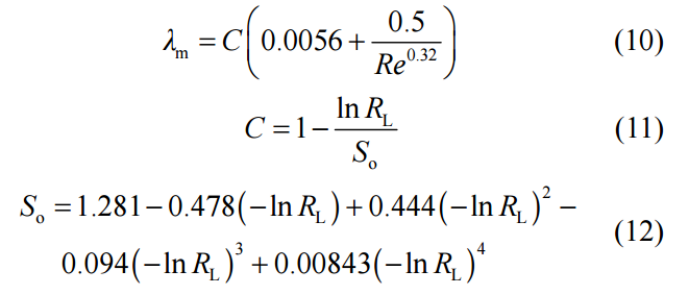
The comparison results between the measured pressure drop values for two types of white oil and the predicted values using the Dukler II method (predicted value II) are shown in Figure 9.

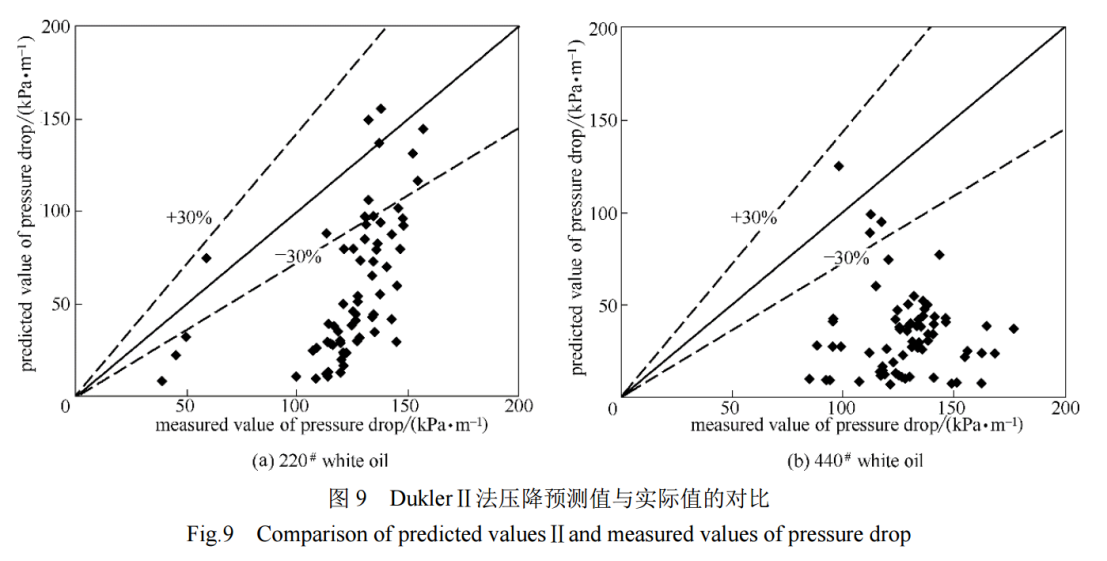
From Figures 8 and 9, it can be seen that when using the Dukler I method, the average relative errors of 220# and 440# white oil are 69.87% and 87.83%, respectively, and the predicted values are smaller than the actual values. This phenomenon becomes more pronounced as the viscosity increases;However, when using the Dukler II method, the average relative errors of 220# and 440# white oils were 54.52% and 72.01%, respectively. Although the predicted values were also smaller than the actual values, the measured values of the two white oils were relatively close to the predicted values, and the smaller the viscosity, the smaller the degree of prediction deviation.The main reason for its crude oil is that, on the one hand, the Dukler II method considers the influence of volumetric and cross-sectional liquid content on its friction coefficient, so the predicted pressure drop is relatively accurate;On the other hand, both the Dukler I and Dukler II methods did not consider the influence of oil viscosity, blending ratio, and other factors on its pressure drop. As the liquid viscosity increases, these factors cannot be ignored. Therefore, when establishing a high viscosity gas-liquid two-phase flow pressure drop model, the influence of viscosity must be considered.

(2) Model Updating

From the above analysis, it can be seen that the predicted values of both pressure drop models are smaller than the actual values. The predicted values calculated by the Dukler I method have a large deviation from the actual values, while the predicted values by the Dukler II method are closer to the actual values.It is known that the Dukler II method is more suitable for predicting the pressure drop of heavy oil blending. Therefore, this article modifies the pressure drop model of the Dukler II method, considers factors such as viscosity and gas-liquid ratio, and uses nonlinear regression to establish a pressure drop model suitable for high viscosity gas-liquid two-phase flow. The pressure drop of the pipeline is calculated using Darcy's formula, mainly to correct its friction coefficient.

Firstly, based on the pressure drop variation law, the blending ratio is divided into three ranges: gas-liquid ratio less than 1.5, gas-liquid ratio between 1.5 and 3.5, and gas-liquid ratio greater than 3.5.

Secondly, a single factor variable analysis was conducted on the experimental results of 220# white oil at various blending ratios. The gas-liquid two-phase flow velocity and density, liquid-phase flow velocity, and volumetric liquid content all affect the friction coefficient of oil and gas two-phase flow.

To further analyze the influence of various factors on the friction coefficient, SPSS software was used to perform variance analysis on the experimental results of each group. It was found that when the gas-liquid ratio was less than 1.5, the liquid phase flow rate and volume fraction had a significant impact on the friction coefficient. When the gas-liquid ratio was between 1.5 and 3.5, the volume fraction had a greater impact on the friction coefficient. When the gas-liquid ratio was greater than 3.5, the volume fraction and gas-liquid ratio had a more significant impact on the friction coefficient.Perform nonlinear regression on various influencing factors to obtain a predictive model for the friction coefficient of oil and gas two-phase flow. The friction coefficient is calculated as follows.

When the gas-liquid ratio is less than 1.5:

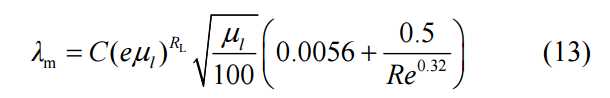
When the gas-liquid ratio is between 1.5 and 3.5:

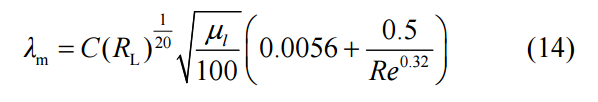
When the gas-liquid ratio is greater than 3.5:

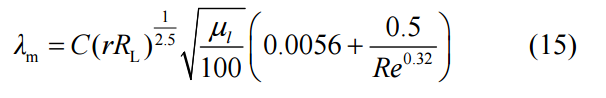
Finally, the predicted pressure drop of 220# white oil was compared with the actual value, as shown in Figure 10 (a). The pressure drop model was validated using experimental data from 440# white oil, and the pressure drop values at each measurement point were calculated and compared with the actual values. The results are shown in Figure 10 (b).

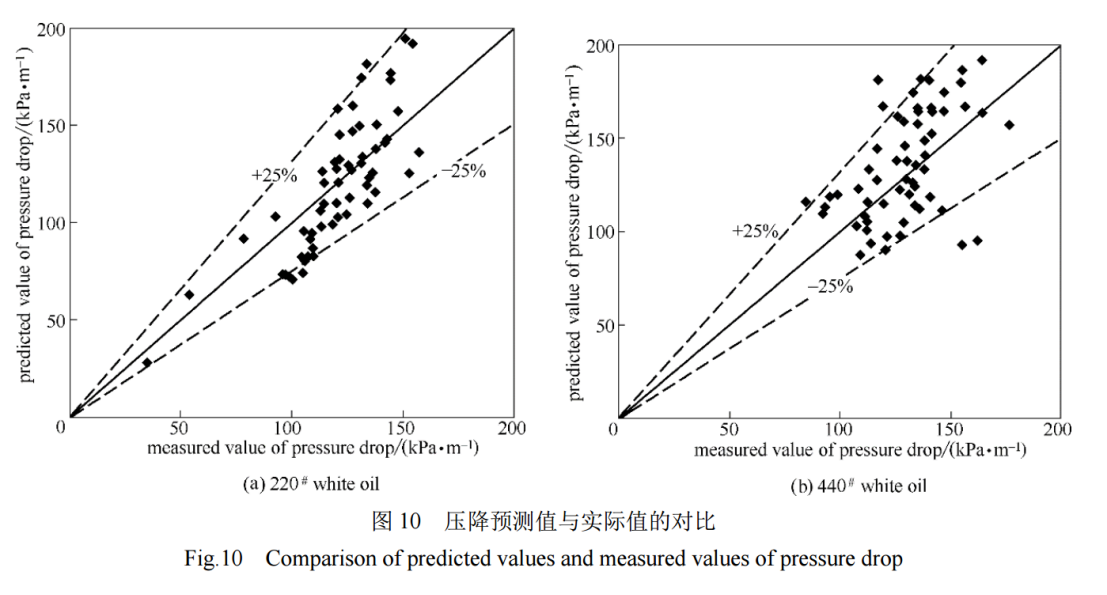
From Figure 10, it can be seen that when using this correction model, the average relative errors between the predicted and actual pressure drop values of 200# and 440# white oil are 15.29% and 16.80%, respectively. Moreover, the deviation between the predicted and actual pressure drop values of more than 95% of the measurement points is within ±25%. The calculated values are in good agreement with the experimental values, which verifies that the model can accurately predict the pressure drop of heavy oil blending, and also verifies that the correction model is applicable to a wide range of viscosity and flow rates. Therefore, when calculating the pressure drop of gas-liquid two-phase flow in high viscosity fluids, it is necessary to consider the effects of liquid phase viscosity and volume fraction.

3. Conclusions

(1).The higher the flow rate of the two types of heavy oil, the higher the pressure drop in the pipeline flow, and the higher the oil viscosity, the greater the pressure drop. As the flow rate of heavy oil increases, the friction resistance coefficient decreases sharply and then tends to flatten out, and the higher the oil viscosity, the greater the friction resistance coefficient. The deviation between the pipe flow simulation results and the rheological test results is small, and the agreement is high.

(2). Under experimental conditions, the maximum drag reduction rate of 220# white oil is 48.19% when the gas-liquid ratio is 1.17# The drag reduction rate of 440# white oil is the highest at a gas-liquid ratio of 0.96, reaching 33.76%. When the gas-liquid ratio is 0.91.2, the drag reduction efficiency of both types of heavy oil by gas blending is higher than 20%; The mechanism can be attributed to the transformation of the oil oil contact surface into oil gas oil contact by air, reducing the interlayer shear stress of the mixed phase.

(3). When the flow rate of white oil is constant, as the gas mixing ratio increases, bubbly flow, slug flow, stratified flow, slug flow, annular flow, and misty flow can be observed in the pipe in sequence; Moreover, as the viscosity of the oil increases, the range of stable laminar flow and the range of other flow patterns become smaller and larger, respectively.

(4). Compared to the Dukler I method, the Dukler II method is more suitable for predicting pressure drop in heavy oil mixed with gas flow. A new model based on the Dukler II method can better predict pressure drop in heavy oil mixed with gas two-phase flow, with an average relative error of less than 20%. In the process of heavy oil recovery and transportation, the accuracy of predicting pressure drop in gas-liquid two-phase flow can be improved.