3.2 Data Preprocessing

The numerical range for pipeline magnetic leakage detection is [-32768, 32767].The large range of numerical variations leads to certain features having a significant impact on model training, resulting in the neglect of other features.Therefore, using deviation normalization (min max) for feature scaling, each element is mapped to the [0,1] interval, and the data deviation normalization process is shown in equation (4).

In the formula, x_i' is the normalized value of data deviation at index i, i is the index of the column where the leakage magnetic data is located, x_i is the initial data, min (X) is the minimum value in data sample X, max (X) is the maximum value, a and b are the minimum and maximum values of the expected deviation standardized interval, respectively. In this article, a and b are set to 0 and 1, respectively.

3.3 Evaluation Indicators

To verify the rationality of the constructed network model, a comprehensive evaluation of the model was conducted using indicators such as accuracy, precision, recall, and F1 value.Accuracy refers to the ratio of correctly identified samples to the total sample; Precision refers to the ratio of the number of correctly identified abnormal samples to the number of identified abnormal samples; Recall rate refers to the ratio of correctly identified abnormal samples to all abnormal samples; The F1 value is a comprehensive indicator of precision and recall.The calculation process is shown in equations (5) - (8).

In the formula, TP represents the number of correctly identified abnormal samples, FP represents the number of incorrectly classified normal samples as abnormal samples, FN represents the number of incorrectly classified abnormal data samples as normal samples, and TN represents the number of correctly identified normal samples. For the task of identifying magnetic leakage anomaly data in oil and gas pipelines, the importance of recall rate ranks first.

3.4 Experimental Comparative Analysis

3.4.1 Comparative Experiments of Different Optimization Methods

Set the Dropout ratio to 0.5 and use two optimization methods, stochastic gradient descent (SGD) and adaptive learning rate (Adam), to observe the training loss function curve of the model (Figure 7).

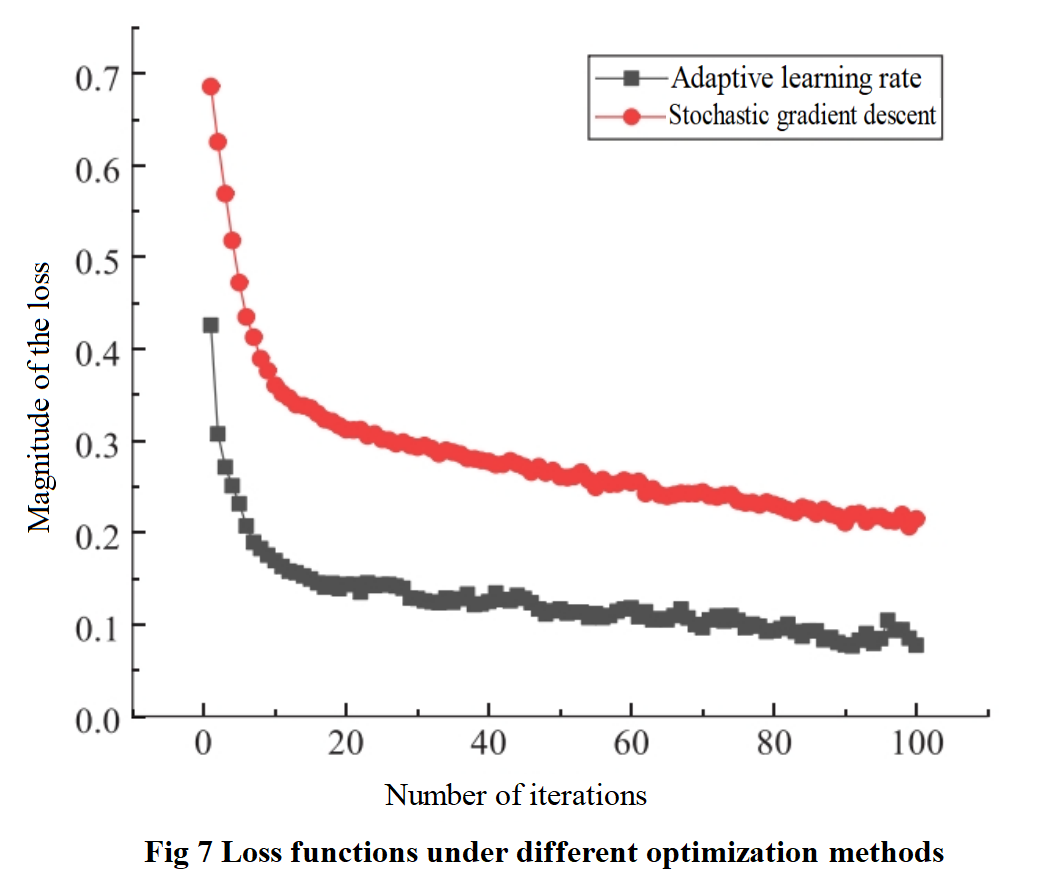
From Figure 7, it can be seen that the training effects of the models using the two optimization methods are different. It is obvious that the SGD optimization method has a slower convergence rate in the early stage of the model, while the Adam optimization method has a better convergence speed than the SGD method. It can achieve better results in a shorter time with lower loss values and stronger fitting ability.

3.4.2 Dropout Comparison Experiment

Using Adam as the optimization method, keeping the remaining hyperparameters constant, observe the model training effect under different Dropout ratios (Figure 8a), and record the loss values and accuracy of the test set under the corresponding Dropout ratios (Table 3). As the training period increases, the gradient tends to zero and the training error tends to be constant (Figure 8a).

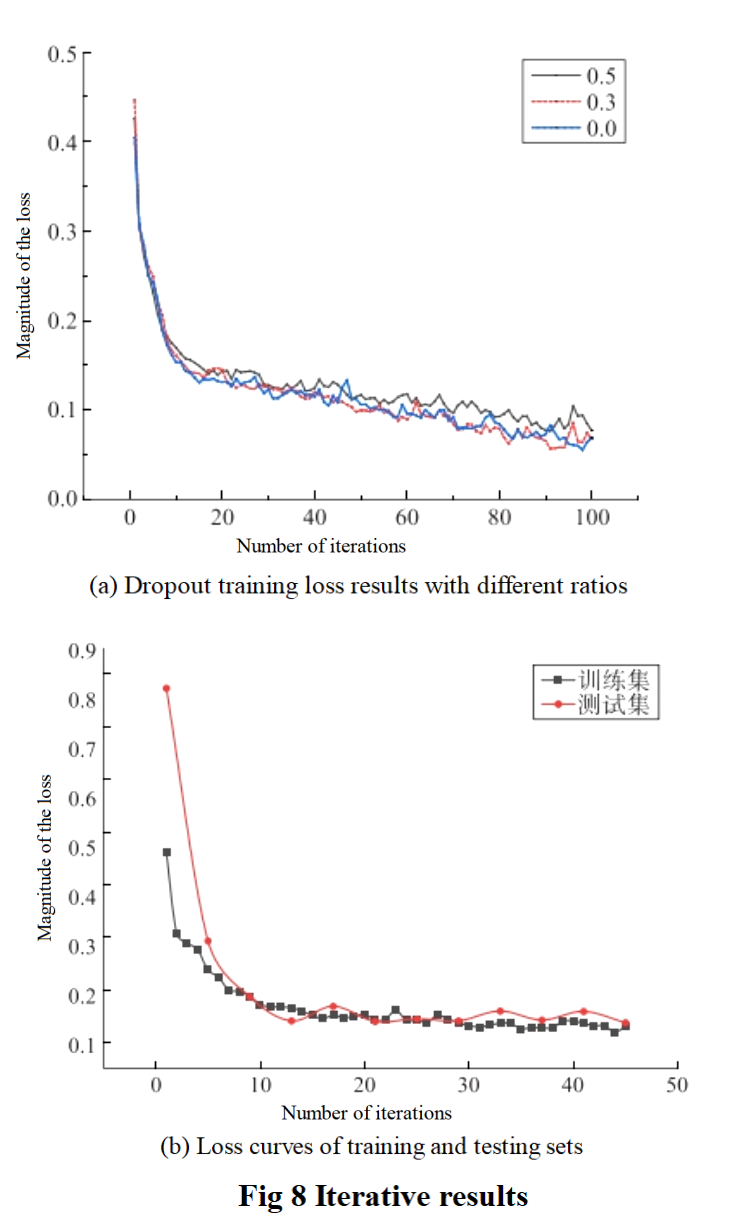
During the training phase, the fitting ability of the model with a Dropout ratio of 0.3 is similar to that of the model without Dropout method, and both are better than the model with a Dropout ratio of 0.5. This indicates that when the Dropout ratio is too large, the fitting ability of the model will be weakened (Figure 8a).The model with a Dropout ratio of 0.3 has lower loss values, higher accuracy, better performance, and more outstanding recognition ability on the test set (Table 3). Overall, it can be concluded that under the Adam optimization method, the model with a Dropout ratio of 0.3 achieved better performance.

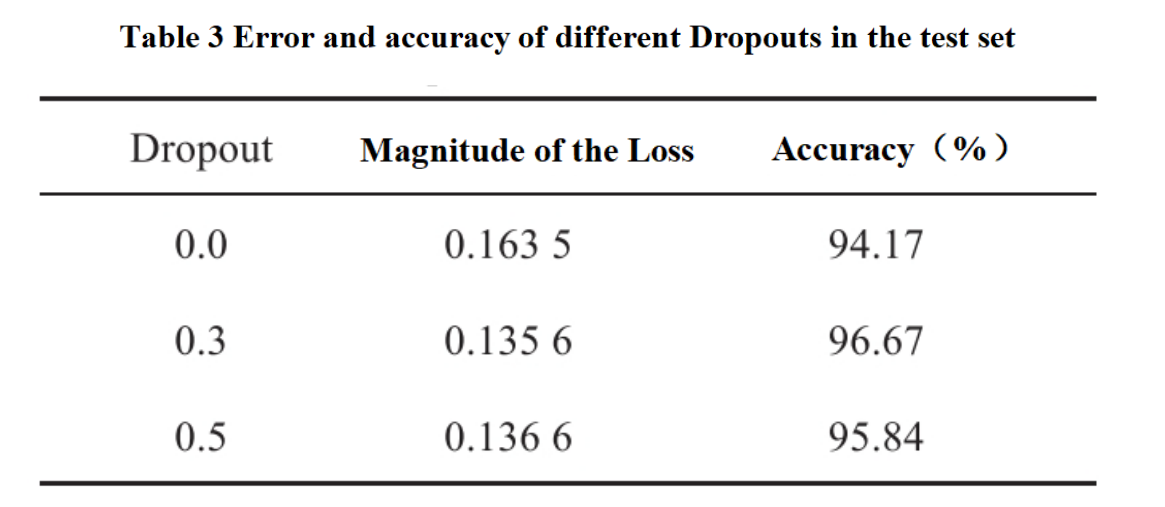
The model is tested every 4 rounds of training, and introducing an early stopping mechanism in the model can help it find a better balance point.Neither overfitting the training data nor oversimplifying it. The parameters of the 45th round of model training are the best (Figure 8b), and the recorded accuracy is 96.73%, precision is 96.73%, recall is 96.67%, and F1 value is 0.96.This model exhibits extremely high precision and recall, indicating that it can effectively identify abnormal samples while significantly reducing the possibility of misclassifying normal samples as abnormal samples.Based on the results of F1 value, the model demonstrates excellent performance in avoiding false positives and false negatives. In addition, with its lightweight design feature, the model has a low memory occupancy rate in the computer, and it only takes 9.96 μs to detect one data sample, thus achieving high recognition efficiency.

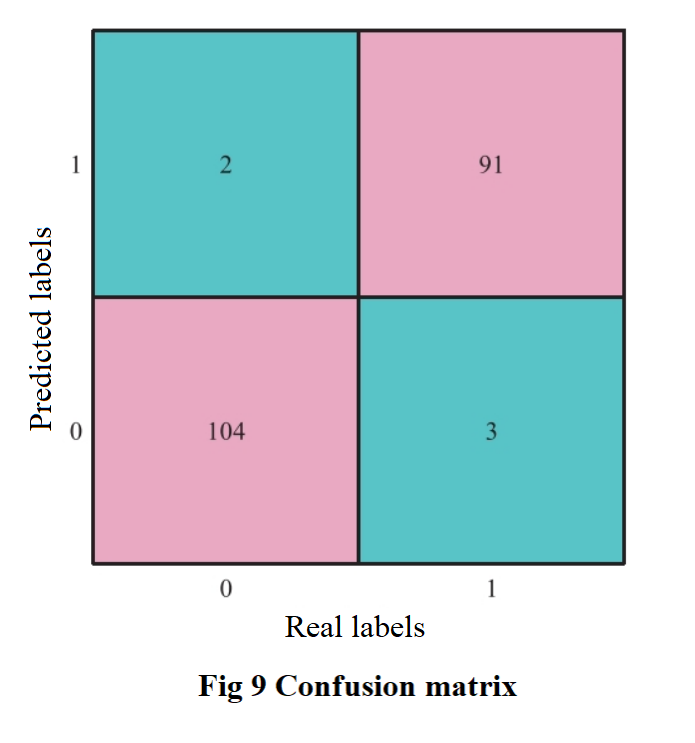
To comprehensively evaluate the feasibility and generalization ability of the model design, a section of leakage magnetic data from a 1219 diameter pipeline file was randomly selected, and the confusion matrix results obtained from the model recognition were observed (Figure 9).A total of 200 leakage magnetic data samples were extracted, and 195 leakage magnetic data samples were accurately identified, including 104 normal data samples and 91 abnormal data samples. Five samples of magnetic flux leakage data were misclassified, including two samples of normal data identified as abnormal data and three samples of missed abnormal data. From the actual test results, it can be seen that the model has high accuracy and good generalization ability.

4. Conclusions

This article proposes an optimized one-dimensional convolutional neural network method for identifying magnetic leakage anomaly data. The one-dimensional convolutional neural network with batch normalization layer and Dropout regularization method has been verified to effectively improve the convergence speed of the model, while also making the model more lightweight.The recall rate on the pipeline testing dataset reaches 96.67%, which has strong data processing advantages compared to manual interpretation and traditional network models, and can provide practical value for the identification, analysis, and processing of magnetic flux leakage data.The method proposed in this article can effectively identify magnetic flux leakage anomaly data in oil and gas pipelines, but it cannot clearly distinguish the type of anomaly it belongs to. In the future, the focus should be on researching methods for identifying anomaly data types.