3.2 数据预处理

管道漏磁内检测数值区间为[-32768，32767]。数值变化范围很大，导致某些特征在模型训练中影响过大，从而忽视其他特征。因此，采用离差标准化（min-max）进行特征缩放，将每个元素映射到[0，1]区间，数据离差标准化过程如式（4）。

式中：x_i′ 为索引i处数据离差标准化后的数值，i为漏磁数据所在列的索引，x_i为初始数据，min（X）为数据样本X中的最小值，max（X）为最大值，a和b分别为所期望的离差标准化区间的最小值与最大值。本文中a和b分别设置为0和1。

3.3 评估指标

为验证所搭建网络模型的合理性，使用准确率（Accuracy）、精度（Precision）、召回率（Recall）和F1值等指标对模型进行全面评估。准确率是指正确识别的样本占总样本的比值；精度是指正确识别异常样本的数量占被识别为异常样本的比值；召回率是指正确识别异常样本的数量占所有异常样本的比值；F1值则是精度与召回率综合后的指标。计算过程如式（5）- 式（8）。

式中：TP为正确识别异常样本的数量，FP为将正常样本错误地分类为异常样本的数量，FN为将异常数据样本错误地分类为正常样本的数量，TN为正确识别正常样本的数量。对于油气管道漏磁异常数据识别任务，召回率的重要性排在首位。

3.4 实验对比分析

3.4.1 不同优化方法的对比实验

将Dropout比率设为0.5，分别采用随机梯度下降（SGD）与自适应学习率（Adam）两种优化方法，观测模型训练损失函数曲线（图 7）。

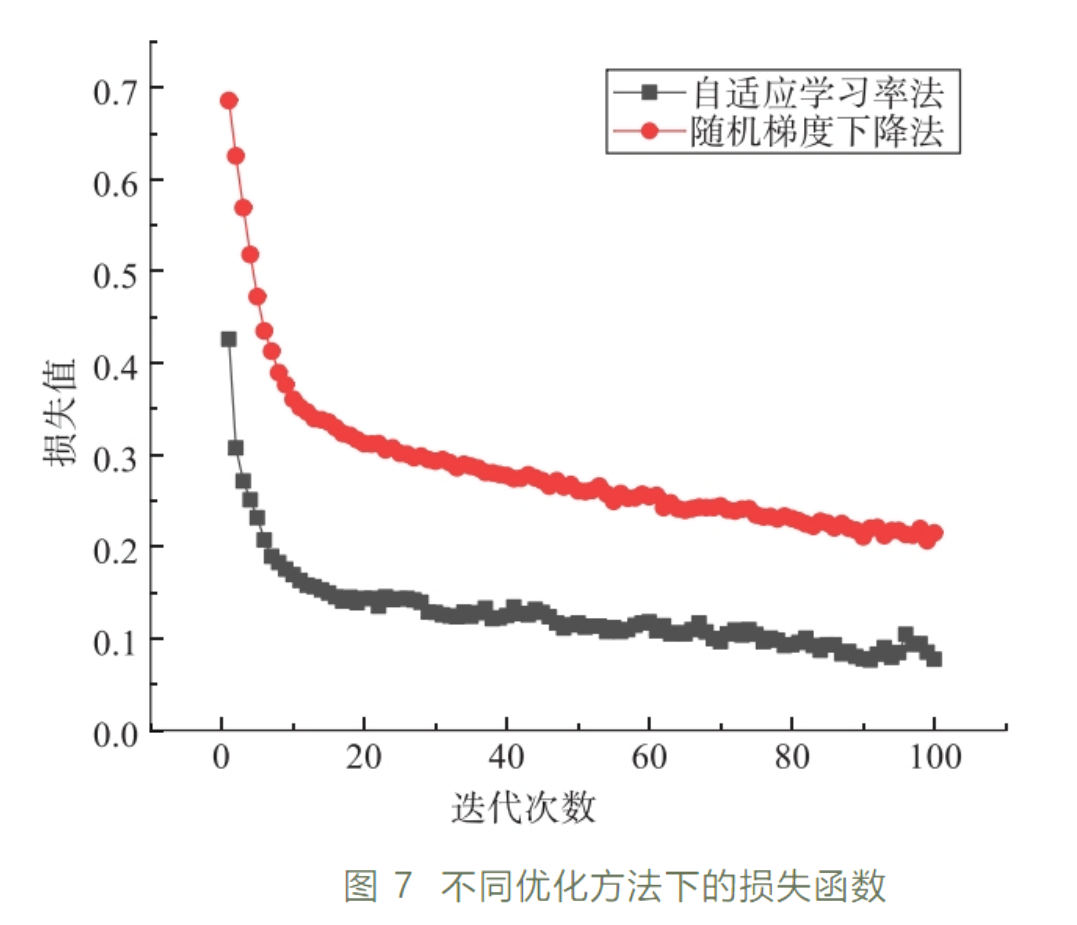
从图 7可知，采用两种优化方法的模型训练效果不同，明显可见采用SGD优化方法模型前期收敛较慢，Adam优化方法对模型的收敛速度优于SGD方法，能够在较短的时间内达到较好的效果且损失值更低，拟合能力更强。

3.4.2 Dropout对比实验

利用Adam作为优化方法，其余的超参数保持不变，观测不同比率的Dropout方法下的模型训练效果（图 8a），记录对应Dropout比率下测试集的损失值和准确率（表 3）。随着训练周期的增加，梯度趋于零，训练误差趋于常数（图 8a）。

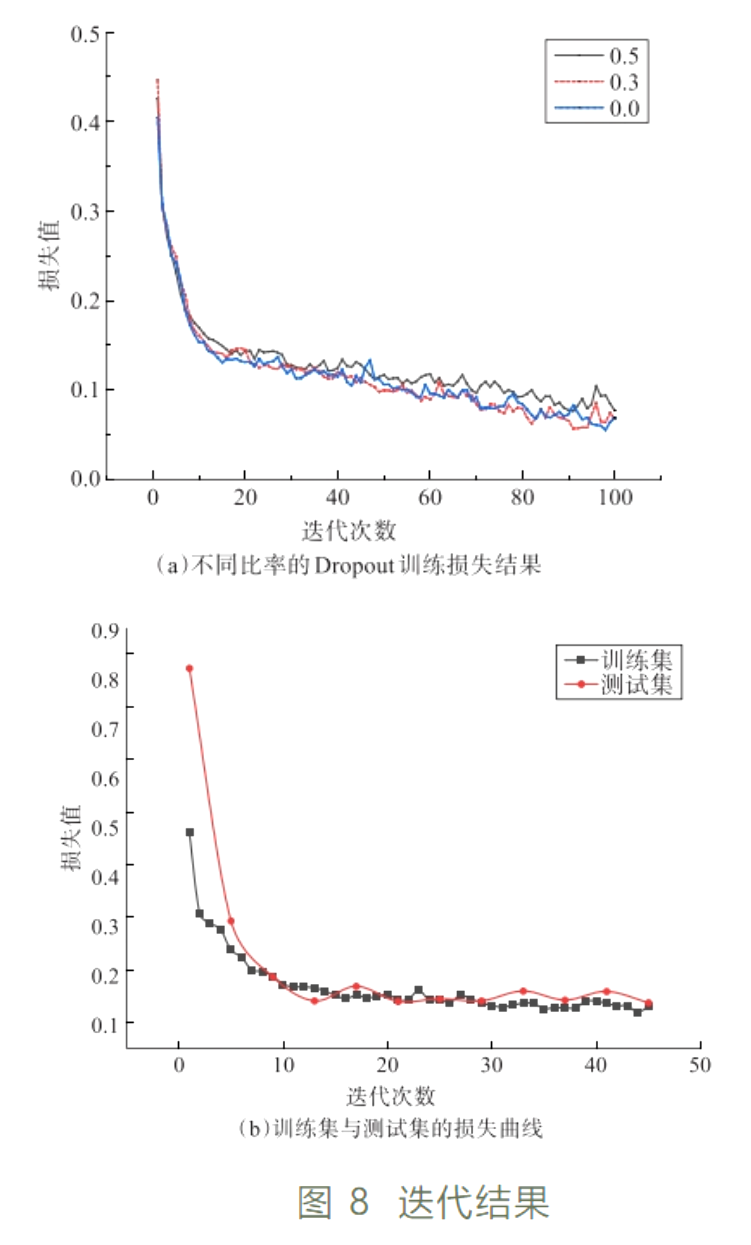
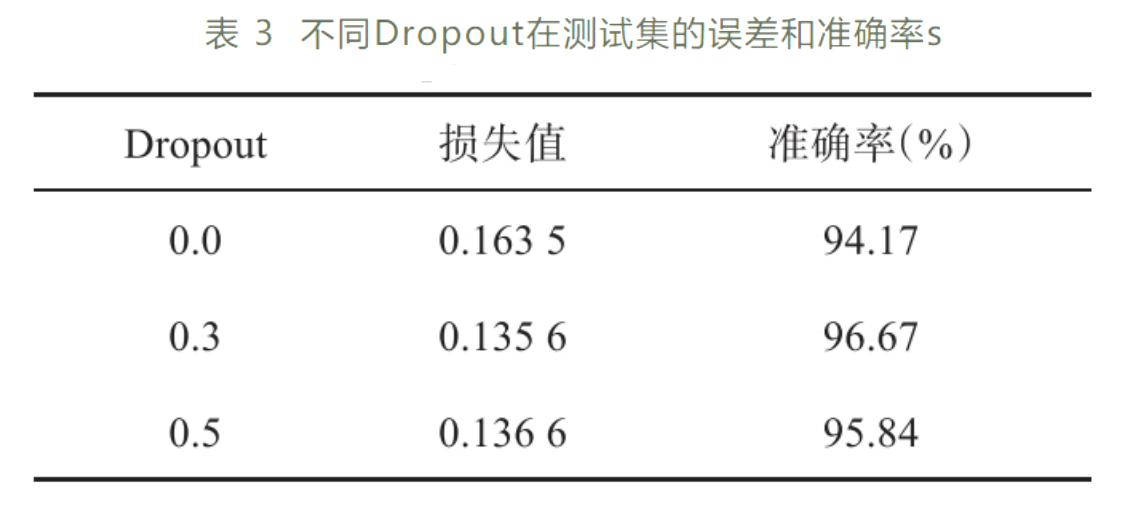
在训练阶段，Dropout比率为0.3的模型与未应用Dropout方法的模型拟合能力较为接近，均优于Dropout比率0.5的模型，表明Dropout比率过大时，模型的拟合能力会被削弱（图 8a）。Dropout比率为0.3的模型在测试集上的损失值更低，准确率更高，表现效果更好，识别能力更突出（表 3）。综合可以得出，在采用Adam优化方法下，Dropout比率为0.3的模型取得了更优的性能效果。

模型每训练4轮测试一次，在模型中引入早停机制，能够帮助模型找到一个更好的平衡点。既不过分拟合训练数据，也不会过于简单化。模型训练第45轮的参数为最佳（图 8b），此时记录下的准确率为96.73%，精度为96.73%，召回率为96.67%，F1值为0.96。该模型展现出极高的精度和召回率，表明其在有效识别异常样本的同时，能够显著减少将正常样本错误地分类为异常样本的可能性。结合F1值的结果，模型在避免漏报和误报方面表现出卓越的性能。此外，凭借其轻量化的设计特点，模型在计算机内存中的占用率较低，检测一个数据样本仅需9.96 μs，从而实现了较高的识别效率。

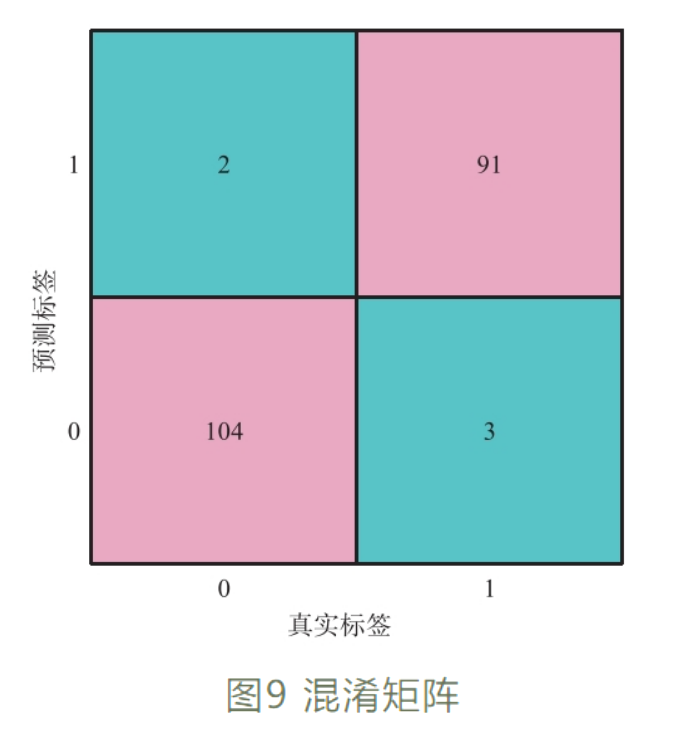
为全面评估模型设计的可行性及其泛化能力，随机选取管径1219管道文件中的某一段漏磁数据，观测模型识别得到的混淆矩阵结果（图 9）。一共抽取200个漏磁数据样本，能够准确识别漏磁数据样本195个，其中正常数据样本104个、异常数据样本91个。误判漏磁数据样本5个，其中误将正常数据样本识别成异常数据样本2个、漏检异常数据样本3个。从实测结果可知该模型具有较高的准确率和较好的泛化能力。

4. 结束语

本文提出了一种优化的一维卷积神经网络识别漏磁异常数据的方法。验证了引入批量归一化层和Dropout正则化方法的一维卷积神经网络，可有效提升模型的收敛速度，同时模型也更加轻量化。在管道测试数据集上的召回率达96.67%，相比人工判读和传统网络模型具有较强的数据处理优势，可以为漏磁数据识别分析处理提供实用价值。本文提出的方法能够有效识别油气管道中的漏磁异常数据，但无法明确区分其所属的异常类别，未来应重点研究异常数据类型的识别方法。